El Número de Oro
El número Phi

EL NÚMERO ÁUREO
El número áureo recibe muchos y misteriosos nombres que despiertan una curiosa fascinación en el oyente: sección áurea, número de oro, razón áurea, media de oro, proporción de oro,… El nombre de divina proporción le fue dado en el siglo XVI por Luca Pacioli en una obra que lleva justo ese nombre, Divina Proportione. Matemáticamente recibe el prosaico nombre de phi (se pronuncia FI), que es la letra griega equivalente a nuestra F, la letra φ. Se le llama así en honor del escultor griego Fidias, quien utilizó mucho esta proporción en su obra.
El número áureo es un número irracional; es decir, un número con infinitos decimales (como el número PI), resultado de una proporción que se encuentra por todas partes en la Naturaleza, lo cual, según algunos la hace especialmente armoniosa y estética a los ojos de los humanos, razón por la cual muchas creaciones artísticas hacen uso de ella, consciente o inconscientemente. Desde la antigüedad obras arquitectónicas, pintura, y música han aplicado la proporción áurea como base de la distribución y composición de las mismas. El pintor Alberto Durero se ocupó de ella en 1525 en su obra Instrucción sobre la medida con regla y compás de figuras planas y sólidas, donde aparece por primera vez la llamada “espiral de Durero” que el artista diseñara mediante regla y compás basándose en la proporción áurea.
Hay quien afirma que el Hombre de Vitrubio, el rostro de la Gioconda y la Última Cena están diseñados utilizando la proporción áurea; e incluso que el propio Partenón fue creado en base al número de oro.
Se dice también que se emplea en marketing para hacer más agradables a la vista determinados productos, como las cajas de cigarrillos.El propio Alberti le dedicó un poema:
A LA DIVINA PROPORCIÓN
A ti, maravillosa disciplina,
media, extrema razón de la hermosura,
que claramente acata la clausura
viva en la malla de tu ley divina.
A ti, cárcel feliz de la retina,
áurea sección, celeste cuadratura,
misteriosa fontana de mesura
que el Universo armónico origina.A ti, mar de los sueños, angulares,
flor de las cinco formas regulares,
dodecaedro azul, arco sonoro.
Luces por alas un compás ardiente.
Tu canto es una esfera transparente.
A ti, divina proporción de oro.
EN EL PENTAGRAMA Y EL PENTÁGONO
La razón áurea está presente en el pentáculo o estrella de cinco puntas; una figura que ha fascinado a muchos desde la más remota antigüedad. De hecho lo encontramos en tablillas sumerias de hace 5200 años; aunque eso no implica que los antiguos sumerios y babilonios conocieran la proporción áurea como han afirmado alegremente algunos. En cualquier caso el pentagrama fascina por su armonía, que se debe según los especialistas en arte, a la presencia en él del número phi. De hecho cada una de las puntas del pentagrama es un triángulo áureo; es decir, un triángulo cuyos lados encierran la razón áurea.
Volvamos a nuestra estrella de cinco puntas. Da igual lo grande o pequeño que sea el pentáculo, en él encontraremos la razón áurea de muchas maneras:
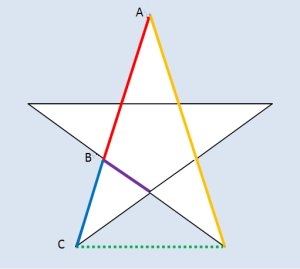
Armémonos de regla, midamos las longitudes de las líneas de color y hagamos las siguientes operaciones:
2. Dividir la línea roja entre la azul
3. Dividir la línea azul entre la violeta
Todas estas operaciones dan el mismo resultado… ¡el número phi!
Si la línea violeta midiera 1, cualquier lado de la estrella, como la línea azul, mediría phi; cada lado de la estrella mediría phi al cubo (el producto de phi por phi por phi); y la suma de un lado de la estrella y de un lado del pentágono del que parten las puntas (línea violeta más línea amarilla), es phi al cuadrado (phi por phi).
Se cumple además que AC/AB da como resultado lo mismo que AB/BC. O lo que es lo mismo; si llamamos “a” a la longitud de AB y “b” a la d de BC:
φ =
(a+b)/a = a/b
Si despejamos a obtenemos una ecuación de segundo grado, que nos permite calcular que el número phi vale:
φ =
(√5+1)/2 = 1.618033988749895...
El resultado es un número de infinitas cifras decimales (irracional). Pese a lo que muchos creen este valor numérico no se conocía en la antigüedad; lo que se conocían eran las propiedades geométricas, las proporciones áureas, no el valor del número.
ALGUNAS PROPIEDADES CURIOSAS
Al inverso de phi (1/phi), se le suele representar como Phi (mayúscula), o mediante la letra fi griega en mayúsculas: Φ. Es decir:
Φ =
1/φ = 0.618033988749895...
Y se da otra curiosa propiedad de este sorprendente número:
φ =
1 + Φ
= 1 + 1/φ
Efectivamente si comparamos los dos valores de PHI y de su inverso:
φ = 1.618033988749895...Φ = 0.618033988749895...
Vemos que basta restarle 1 al número de oro para obtener su inverso.
Además es el único número real que cumple que al multiplicarse por si mismo es igual a él mismo más 1: phi al cuadrado es igual a phi más 1:
φ2
= φ + 1
Es posible relacionar phi y PI (π) empleando funciones trigonométricas:
φ =
2cosπ/5)
Una curiosidad que relaciona el famoso número de la bestia con phi:
sen(666)
= -φ/2
También resulta curioso como el número áureo, y su inverso, pueden expresarse en forma recursiva:

En la primera fórmula vemos como puede expresarse phi mediante fracciones recursivas; la segunda forma nos muestra el modo en que puede expresarse su inverso, Phi. La última forma expresa fi de forma recursiva mediante raices cuadradas.
PHI Y LA SECUENCIA DE FIBONACCI
El número phi está profundamente relacionado con la secuencia de Fibonacci. Fibonacci (Leonardo de Pisa), fue un matemático italiano del siglo XIII que describió una secuencia de números, conocida ya por matemáticos hindúes, mediante los cuales se llegaba a phi.
Dicha secuencia es ésta: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

Leonardo de Pisa, Fibonacci
Para obtenerla partimos de 0 y 1 y vamos colocando a la derecha el resultado de sumar los dos últimos números de la serie:
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
…
¿Qué tiene qué ver esto con phi? Hay infinitos números en la serie. Si dividimos un número de la serie de Fibonacci por el que le precede en la serie obtenemos un número que se aproxima a phi tanto más cuanto mayor es el número de la secuencia escogido para dividir por el que le precede. Así si llamamos n a la posición de un número en la serie, cuando n tiende a infinito el cociente entre el número de la serie en la posición n y el que le precede es phi. Matemáticamente se expresa así:
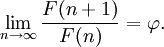
Cualquier número de la serie puede predecirse utilizando phi:
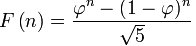
Donde n es la posición que ocupa el número en la serie.
La serie de Fibonacci se emplea muchísimo en Matemáticas y ciencia de la computación, y aparece en la descripción de muchos fenómenos físicos y naturales, incluyendo la Biología. Por ejemplo Kepler hablaba de ella en su De Nive Sexángula mostrando su relación con phi y aplicándola al crecimiento de las plantas.
Por ejemplo, los brazos de las galaxias, o el dibujo de las conchas de caracol, la distribución de pétalos de flores, pipas en un girasol, piñones en una piña, etc. Muchas espirales de la naturaleza se inscriben en cuadrados cuyos lados siguen las medidas de la serie de Fibonacci. La concha de un Nautilus, el famoso fósil viviente, se inscribe así en cuadrados cuyos lados tienen de longitud los números de la serie:
Espiral inscrita en cuadrados de Fibonacci
Los números de la secuencia de Fibonacci describían, como observó Leonardo de Pisa, el número de conejos que tenemos en sucesivas crías a partir de uno. Pero los números de la secuencia aparecen también en otros muchos ejemplos naturales; por ejemplo, el número de pétalos de la gran mayoría de las flores es un número de la serie.
EL RECTÁNGULO ÁUREO
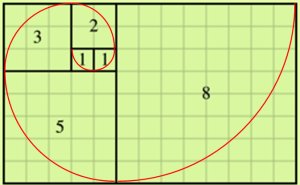
El conocido matemático griego Euclides, que vivió en el siglo IV a.C. describió en su obra Elementos como crear un rectángulo áureo. Dibujamos un cuadrado de dos unidades de lado. Tomamos un compás y lo situamos en la mitad de uno de ellos (en la figura marcado como G), y trazamos un arco de circunferencia de radio GC (línea azul punteada):
El rectángulo áureo
Obtenemos así el segmento BE, a partir del cual podemos dibujar el rectángulo BEFC, un rectángulo áureo. Se le llama así porque su lado mayor dividido por su lado menor es exactamente el número phi. Por otra parte el rectángulo AEFD es otro rectángulo áureo. Si miramos bien, seguro que encontramos una gran cantidad de objetos a nuestro alrededor que responden a estas proporciones.
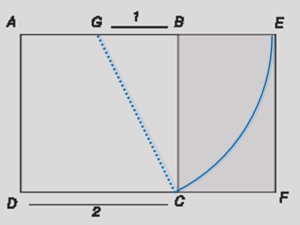
EL ÁNGULO DE ORO
Se llama el ángulo de oro al ángulo más pequeño resultante de dividir una circunferencia en dos ángulos de modo que el cociente entre ambos se phi. Si lo calculamos su valor es aproximadamente 137.51° ó 2.399963 radianes. El ángulo dorado aparecería en algunas formaciones naturales asociadas a formas circulares; especialmente en la disposición de los pétalos de ciertas flores, y particularmente en los girasoles, cuyas semillas se alinean formando una espiral de Fermat, basada en la secuencia de Fibonacci.
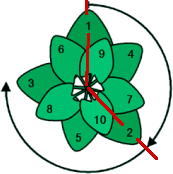
A la izquierda, el ángulo de oro (en rojo). A la derecha, el ángulo de oro en la disposición de pétalos de una flor.
VERDADES Y MENTIRAS SOBRE EL NÚMERO DE ORO
El Código Da Vinci, de Don Brown ha popularizado el número de oro, φ. No obstante este famoso best seller contiene una importante cantidad de errores que han contribuido a oscurecer más que a aclarar muchos de los variopintos temas tratados en la obra. Veamos algunos en relación con la sección áurea y la serie de Fibonacci:
En el libro se afirma que Fibonacci fue el creador de la serie que lleva su nombre. Cualquier aficionado a las matemáticas sabe que eso no es cierto. Fibonacci conoció la serie gracias a los matemáticos árabes, los cuales a su vez la conocían gracias a matemáticos hindúes.
Brown además afirma que el cociente entre el número de abejas macho y el de abejas hembra "en cualquier panal del mundo" es phi. Es una afirmación absurda. Esta proporción varía continuamente, pero nunca es phi. En otoño los zánganos, que ya cumplieron su cometido, son expulsados de la colmena y mueren. En primavera y verano vuelven nacen más zánganos, pero la proporción nunca es la razón áurea. Por una reina suele haber entre 300 y 1000 zánganos; y entre 45000 a 55000 hembras, las abejas obreras. Es evidente que ninguna de estas cantidades permite descubrir la proporción áurea.
Desde mucho antes que Brown diferentes investigadores han buscado la proporción áurea en todo tipo de construcciones, esculturas, pintura, música, etc.; incluidas las pirámides de Egipto, los cuadros de Leonardo, la catedral de Chartres, el Partenon de Atenas, etc. Hay una abundante bibliografía acerca de la "Geometría Sagrada". En algunos casos se ha recurrido a "encajar" de modo muy rebuscado dichas obras en patrones asociados a la proporción; y es este un terreno abonado para la especulación. No cabe duda, sin embargo, de que muchas obras de arte lo aplican, consciente o inconscientemente como ya apuntamos. Es muy posible que muchos artistas, aún sin saberlo, lo hayan aplicado sencillamante llevados por su singularidad estética.
VÍNCULOS DE INTERÉS
- Una excelente página en inglés muy completa sobre phi en Aritmética y Geometría, aquí.
- Algunos vídeos sobre Phi en Youtube:
Como resolver la ecuación de segundo grado que permite obtener el valor de phi
© 2008. Del texto y traducciones, Javier Arries